RATIO – PROPORTION – VARIATION

1. If a : b : : c : d, then ad = bc

2. If a : b : : c : d, then a + b : b : : c + d : d

3. If a : b : : c : d, then a - b : b : : c - d : d

4. If a : b : : c : d, then a + b : a - b : : c + d : c - d

5. If then k =

NUMBERS

1. a³ + b³ + c³ – 3abc = (a + b + c) (a² + b² + c² – ab – bc – ca)

2. The product of n consecutive integers is always divisible by n! (n factorial)

3. The sum of any number of even numbers is always even

4. The sum of even number of odd numbers is always even

5. The sum of odd number of odd numbers is always odd

6. If N is a composite number such that N = a^p . b^q . c^r .... where a, b, c are prime factors of N and p, q, r .... are positive integers, then

a) the number of factors of N is given by the expression (p + 1) (q + 1) (r + 1) ...

b) it can be expressed as the product of two factors in 1/2 {(p + 1) (q + 1) (r + 1).....} ways

c) if N is a perfect square, it can be expressed

(i) as a product of two DIFFERENT factors in 1/2 {(p + 1) (q + 1) (r + 1) ... -1 } ways

(ii) as a product of two factors in 1/2 {(p + 1) (q + 1) (r + 1) ... +1} ways

d) sum of all factors of N =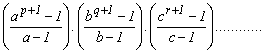

e) the number of co-primes of N (< N), f (N) =

f) sum of the numbers in (e) =

g) it can be expressed as a product of two factors in 2^n–1, where ‘n’ is the number of different prime factors of the given number N

SIMPLE INTEREST AND COMPOUND INTEREST

I = Interest, P is Principle, A = Amount, n = number of years, r is rate of interest

1. Interest under

a) Simple interest, I =

b) Compound interest, I = P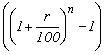

2. Amount under

a) Simple interest, A =

b) Compound interest, A = P

3. Effective rate of interest when compounding is done k times a year

r_e =

MIXTURES AND ALLIGATION

1. If p₁, p₂ and p are the respective concentrations of the first mixture, second mixture and the final mixture respectively, and q₁ and q₂ are the quantities of the first and the second mixtures respectively, then Weighted Average (p)

p =

2. If C is the concentration after a dilutions, V is the original volume and x is the volume of liquid. Replaced each time then C =

QUADRATIC EQUATIONS

1. If a, b and c are all rational and x +is an irrational root of ax² + bx + c = 0, then x - is the other root

2. If a and b are the roots of ax² + bx + c = 0, then a + b =and ab =

3. When a > 0, ax² + bx + c has a minimum value equal to, at x =

4. When a < 0, ax² + bx + c has a maximum value equal to, at x =

PROGRESSIONS

Arithmetic Progression (A.P)

a is the first term, d is the last term and n is the number of terms

1. T_n = a + (n – 1)d

2. S_n = =

3. T_n = S_n – S_n-1

4. S_n = A.M ´ n

Geometric Progression (G.P)

a is the first term, r is the common ratio and n is the number of terms

5. T_n = ar^n-1

6. S_n = =

Harmonic Progression (H.P)

7. H.M of a and b =

8. A.M > G.M > H.M

9. (G.M)² = (A.M) (H.M)

10. Sum of first n natural numbers ån =

11. Sum of squares of first n natural numbers ån² =

12. Sum of cubes of first n natural numbers ån³ == (ån)²

GEOMETRY

1. In a triangle ABC, if AD is the angular bisector, then

2. In a triangle ABC, if E and F are the points of AB and AC respectively and EF is parallel to BC, then

3. In a triangle ABC, if AD is the median, then AB² + AC² = 2(AD² + BD²)

4. In parallelogram, rectangle, rhombus and square, the diagonals bisect each other

5. Sum of all the angles in a polygon is (2n – 4)90

6. Exterior angle of a polygon is

7. Interior angle of a polygon is

8. Number of diagonals of a polygon is

9. The angle subtended by an arc at the centre is double the angle subtended by the arc in the remaining part of the circle

10. Angles in the same segment are equal

11. The angle subtended by the diameter of the circle is 90°

MENSURATION

1. Plane figures

2. Solids

HIGHER MATHS – I

(PERMUTATIONS & COMBINATIONS, PROBABILITY)

1. n (A È B) = n (A) + n (B) – n (A Ç B)

2. If A and B are two tasks that must be performed such that A can be performed in 'p' ways and for each possible way of performing A, say there are 'q' ways of performing B, then the two tasks A and B can be performed in p ´ q ways

3. The number of ways of dividing (p + q) items into two groups containing p and q items respectively is

4. The number of ways of dividing 2p items into two equal groups of p each is , when the two groups have distinct identity and , when the two groups do not have distinct identity

5. ⁿC_r = ⁿC_{n– r}

6. The total number of ways in which a selection can be made by taking some or all out of (p + q + r + .....) items where p are alike of one kind, q alike of a second kind, r alike of a third kind and so on is {(p + 1) (q + 1) (r + 1) ....} -1

7. P(Event) = and 0 £ P(Event) £ 1

8. P(A Ç B) = P(A) ´ P(B), if A and B are independent events

9. P(A È B) = 1, if A and B are exhaustive events

10. Expected Value = [Probability (E_i)]´ [Monetary value associated with event E_i]

HIGHER MATHS – II

(STATISTICS, NUMBER SYSTEMS, INEQUALITIES & MODULUS, SPECIAL EQUATIONS)

1. G.M. = (x₁ × x₂ × ...... .x_n)^1/n

2.

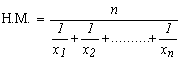
3. For any two positive numbers a, b

(i) A.M. ³ G.M. ³ H.M. (ii) (G.M.)² = (A.M.) (H.M.)

4. Range = Maximum value – Minimum value

5. Q.D. =(i.e., one-half the range of quartiles)

6. If a > b, , for any two positive numbers a and b

7. |x + y| £ |x| + |y|, for any two real numbers x and y

8. If for two positive values a and b; a + b = constant (k), then the maximum value of the product ab is obtained for a = b =

9. If for two positive values a and b; ab = constant (k), then the minimum value of the sum (a + b) is obtained for a = b
=

HIGHER MATHS – III

(CO-ORDINATE GEOMETRY, FUNCTIONS & GRAPHS, TRIGONOMETRY)

1. If a point P(x, y) divides the line segment joining A(x₁, y₁) and B(x₂, y₂) in the ratio m : n, then x =and y =, positive sign for internal division and negative sign for external division

2. The area of a triangle with the vertices at (0, 0), (x₁, y₁) and (x₂, y₂) is D = .

3. The coordinates of the centroid C(x, y) of a triangle ABC formed by joining the points
A(x₁, y₁); B(x₂, y₂) and C(x₃, y₃) are given by

4. The slope of line with points (x₁, y₁) and (x₂, y₂) lying on it is m =

5. If m₁ and m₂ are the slopes of two lines L₁ and L₂ respectively, then the angle ‘q’ between them is given by tanq =

6. The equation of the x-axis is y = 0 and that of y-axis is x = 0

7. The equation of a line parallel to x-axis is of the form y = b and that of a line parallel to y-axis is of the form x = a (a and b are some constants)

8. Point slope form of a line: y – y₁ = m (x – x₁)

9. Two point form of a line:

10. Slope intercept form of a line: y = mx + b

11. Intercept form of a line :

12. Two lines a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 are

(i) parallel if or m₁= m₂

(ii) perpendicular if a₁ a₂ + b₁ b₂ = 0 or m₁ m₂ = -1

13. The distance between two parallel lines of the form ax + by +c₁ = 0 and ax + by + c₂ = 0 is given by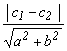

14. If ax + by + c = 0 is the equation of a line, then the perpendicular distance of a point (x₁, y₁) from the line is given by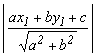

15. sine rule : = 2R, where R is the circumradius of triangle ABC

16. cosine rule : cosA =, similarly cosB and cosC can be defined